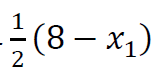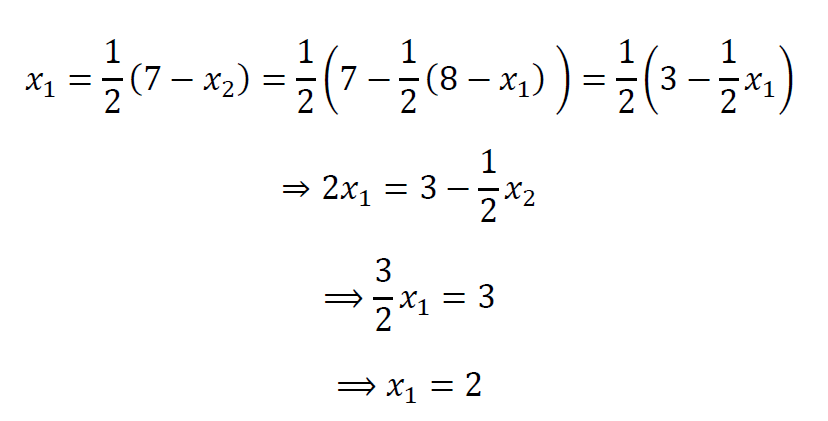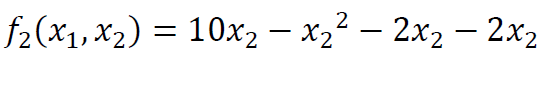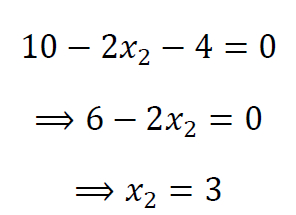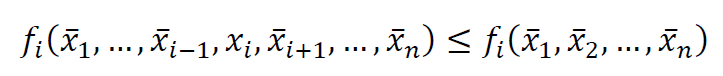گامی کوچک اما شیرین در نظریه بازی ها

اگر بخواهیم به طور خلاصه بگوییم که نظریه بازیها چیست، باید بگوییم که:

نظریه بازیها به مطالعه ی وضعیت هایی می پردازد که در آنها چند تصمیم گیرنده وجود دارد و قصد این تصمیم گیرنده ها از اتخاذ تصمیمشان رسیدن به بیشترین سود است. در ضمن سودی که در پایان نصیب هر کدام می شود نه تنها به تصمیم خودش بلکه به تصمیماتی که دیگران اتخاذ کرده اند نیز بستگی دارد. همچنین آنان کاملا منطقی عمل می کنند و به عقلایی بودن یکدیگر کاملا واقف اند.

به این وضعیت ها بازی می گوییم و به این تصمیم گیرنده ها بازیکن اطلاق میشود.

به انتخاب ها یا تصمیماتی که هر بازیکن می تواند اتخاذ کند، استراتژی آن بازیکن می گوییم.

قصد ما در اینجا بررسی نوعی از بازی در نظریه بازیها است که دارای ویژگی های زیر می باشد:

الف . بازی ایستا است به این معنی که بازی در یک مرحله انجام میگردد و تصمیمات بازیکنان به طور هم زمان اتخاذ می شود.

ب . بازی غیرمشارکتی است به این معنی که بازیکنان به هیچ وجه نمی توانند با هم تبادل نظر یا مذاکره ای داشته باشند و به توافقی برسند و یا به ائتلافی دست بزنند.

فرض کنید {𝐼={1,2,…,𝑛 مجموعه ی بازیکنان یک بازی باشد (بازیکنان با شماره مشخص شده اند) ومجموعه ی استراتژیهای بازیکن 𝑖 ام را با X_i  نشان دهیم. هر بازیکن در جریان بازی باید یک استراتژی را از مجموعه ی استراتژی هایش انتخاب کند و سود یا بازدهی او به استراتژیهای که خودش و دیگران انتخاب می کنند بستگی دارد، پس تابعی از 𝑛 متغیر است.

ج. سود هر بازیکن در بازی با یک عدد حقیقی نشان داده میشود.

بنابراین تابع بازدهی هر بازیکن مثلا بازیکن 𝑖 ام به صورت 

 است.

د. بازی با اطلاعات کامل است به این معنی که هر بازیکن از تعداد بازیکنان، مجموعه ی استراتژی ها و توابع بازدهی آنان با خبر است.

مثال یک: یک بازی دو نفره را در نظر بگیرید که:

مجموعه ی استراتژی های بازیکن شماره ی 1 ، 𝑋1={𝑥1,𝑥2}  و

مجموعه ی استراتژی های بازیکن شماره 2، 𝑌1={𝑦1,𝑦2} باشد. میزان سود هر بازیکن را با توجه به استراتژی ای که خودش و دیگری انتخاب می کند را در جدول زیر نشان می دهیم:

(یعنی اگر بازیکن 1 استراتژی 𝑥2 را انتخاب کند و بازیکن 2 استراتژی 𝑦1 را انتخاب کند، سود بازیکن 2برابر 0 و سود بازیکن 1 برابر 400 خواهد بود)

روشن است که هر بازیکن سعی دارد به بیشترین سود دست پیدا کند. حال اگر شما جای بازیکن 1 بودید چه می کردید؟ کدام استراتژی را انتخاب می کردید؟ 𝑥1 یا 𝑥2 را؟

شاید بگویید که من استراتژی 𝑥2 را انتخاب می کنم، چون در هر صورت (بازیکن 2 هر استراتژی را انتخاب کند) سود من در انتخاب 𝑥2 بیشتر از انتخاب 𝑥1 است. این انتخاب به خاطر "عقلانیت فردی" شماست. شما استراتژی 𝑥1 را به عنوان "استراتژی مغلوب" کنار گذاشتید.

اما سود شما در انتخاب این استراتژی واقعا چیست؟ شما به سود 400 دست پیدا خواهید کرد یا 100 ؟

روشن است که بازیکن 2 نیز از همین میزان عقلانیت فردی برخوردار است (در نظریه بازیها فرض بر این است که تمام بازیکنان کاملا منطقی و عقلایی هستند)، پس بازیکن 2 نیز باید استراتژی 𝑦2 را انتخاب کند!

این یعنی سود شما 100 خواهد بود نه 400 !

شما تمام این نتیجه گیری ها را پیش خودتان انجام دادید، چون هم شما عاقل هستید و هم نفر مقابلتان را عاقل می دانید ) این همان فرضی است که نظریه بازیها بر آن استوار است(.شاید پیش خودتان بگویید که ای کاش هر دو استراتژی اولمان را انتخاب می کردیم! اما این فقط در حد ایکاش باقی خواهد ماند، چون در این بازی شما نمی توانید با هم گفتگویی داشته باشید و یا به توافقی برسید (بازی غیر مشارکتی است). در این شرایط چطور می توانید به هم اعتماد کنید؟

اگر شما استراتژی 𝑥1 را انتخاب کنید باید انتظار سود صفر را نیز داشته باشید که این دور از عقل است.

البته در شرایطی بنا را بر اعتماد می گذارند که آن هم اصول خاص خودش را دارد و در بازیهایی که در دفعات زیاد تکرار می شود صورت می گیرد که در اینجا بررسی نمیگردد.

مثال دو: فرض کنید یک بازی دو نفره داشته باشیم که مجموعه ی استراتژی های هر بازیکن، مجموعه ی اعداد حقیقی و تابع بازدهی بازیکنان به صورت زیر باشد:

حال اگر شما جای بازیکن شماره ی 1 باشید، چه استراتژی را انتخاب می کنید؟ به عبارت دیگر چه مقدار حقیقی برای 𝑥1 در نظر میگیرید؟

شما می دانید که مقدار 𝑥2 را نخواهید فهمید تا این که خودتان استراتژیتان را انتخاب کنید! پس با دلخواه درنظر گرفتن استراتژی نفر دوم، باید استراتژی خودتان را طوری انتخاب کنید که بازدهی شما حداکثر شود.

بنابراین نسبت به متغیر 𝑥1 از تابع بازدهی خودتان مشتق میگیرید و برابر صفر قرار می دهید:

پس اگر نفر دوم استراتژی 𝑥2 را انتخاب کند، بهترین انتخاب برای شما

خواهد بود.

همچنین اگر شما استراتژی 𝑥1 را انتخاب کنید، بهترین واکنش نفر دوم انتخاب استراتژی

 

خواهد

بود (چون نفر دوم هم به اندازه ی خود شما منطقی است، همین نتیجه گیری را پیش خودش خواهد کرد و شما هم که از عاقل بودن او مطمئن هستید این نتیجه گیری او را میدانید!)

پس شما استراتژی 𝑥1 را به این صورت انتخاب می کنید:

همچنین نفر دوم هم به همین صورت عمل خواهد کرد و او نیز 𝑥2=3 انتخاب می کند.

نکتهی مهم: اگر شما استراتژی 𝑥1=2 انتخاب کنید، بهترین واکنش نفر دوم این بوده که استراتژی 𝑥2 را طوری انتخاب کند که تابع

 حداکثر شود.

یعنی

پس انتخاب 𝑥2=3 بهترین واکنش نفر دوم نسبت به انتخاب استراتژی 𝑥1=2 از طرف شماست و

همچنین می توانید ببیند که در برابر انتخاب استراتژی 𝑥2=3 از طرف بازیکن دوم، بهترین واکنش شما هم انتخاب استراتژی 𝑥1=2 خواهد بود.

به نقطه ی (2,3) یک تعادل نش در این بازی می گویند.

تعریف تعادل نش:

فرض کنید که (𝑥̅1,𝑥̅2,…,𝑥̅𝑛) مجموعه ی خاصی از استراتژی ها باشد که توسط 𝑛 بازیکن اتخاذ میشود.

این نقطه را یک تعادل نش برای بازی می نامند هرگاه به ازای هر {𝑖∈{1,2,…,𝑛 بهترین واکنش بازیکن 𝑖 ام در برابر انتخاب استراتژی  𝑥̅j   که  (𝑗≠𝑖)

 توسط سایر بازیکنان، انتخاب استراتژی 𝑥̅𝑖 باشد. به عبارت دیگر به

ازای هر 𝑖 و هر استراتژی 𝑥𝑖∈𝑋𝑖 ، داشته باشیم:

در این صورت (𝑥̅1,𝑥̅2,…,𝑥̅𝑛) را یک تعادل نش برای بازی میگویند.

می توانید ببینید که در مثال اول هم نقطه ی (𝑥2,𝑦2) تعادل نش در بازی بود.

ذهن زیبا

یادم است وقتی از پایان نامه ی خودم دفاع می کردم چه حس و حالی داشتم.

سوالی ذهن من رو درگیر کرده بود:

ما چه می کنیم؟ این پایان نامه به چه دردی میخورد؟ خط فکری از کجا آغاز شده و به کجا نهایت میپیوندد.

مسیر فکری همیشه در مطالعه و تحقیق برای من مهم بود. اینکه قصد من چیست؟

قرار هست کوهی از تعریف ارائه بدهم و قضیه اثبات کنم؟

قدرت استدلالی که من آن را مدیون مطالعه ی جبر هستم قرار است در همین محدوده بماند و به ارائه تعاریف جدید و اثبات احکام مربوط کننده ی این تعاریف ختم شود؟

همان سال با استادی آلمانی که در دانشگاه ما کنفرانسی ارائه میداد رو به رو شدم.

وقتی از او پرسیدم: محض یا کاربردی؟ دنبال بیان تعاریف به راه خود ادامه دهیم بدون نگاه به اطراف و یا باید با توجه به کاربرد حرکت کنیم؟

او گفت: در کشور من هر دو گروه مشغول به کار هستند. من خودم از محض به کاربردی رفتم و شرکت هایی هم هستند که از ریاضیدانان متخصص در موضوعات محض و مجرد برای استدلال کردن در مباحث کاربردی مورد نظر شرکت بهره می برند

در پایان دستش را روی قلبش گذاشت و گفت:

هر چه دلتان میگوید. مهم قلبتان است

و من

و من چقدر دوست داشتم جزو ریاضیدانانی بودم که به خاطر قدرت استدلالم در مباخث کاربردی تر مشغول کار می شدم.

اما چطور؟

کجا؟

من آنالیز عددی دوست ندارم حتی فکرش را هم نمیتوانستم بکنم مهارتم را باید در روشهای عددی برای به دست آوردن جواب معادلات و .. به کار ببرم.

من چیزی میخواستم که ارتباط با جهان پیرامونم داشته باشد و منطق و استدلال کردن در ان کلید تعیین کننده باشد. چیزی که از هر دو سو قابل تعمیق بخشیدن باشد.

وقتی منطق را در نظر بگیرم بتوانم خودم را در اقیانوسی عمیق غوطه ور ببینم و وقتی کار به پیدا کردن پاسخ برای مشکلات واقعی برسد، من خودم را با قویترین و زیباترین ابزار ریاضی ببینم. کسی که به کار می آید نه فقط سخنرانی یا چیزهای دیگر

و خداوند همیشه پاسخگوی قلب های مشتاق است:

پروفسور علیمحمدی مدیر گروه ریاضی دانشگاه مازندران موضوعی را رو به روی من قرار داد:

نظریه ی بازیها

البته موضوعات دیگری را هم رو به روی من قرار داد ولی آنچه جالب بود این بود که استاد فرمودند:

آیا فیلمی که راسل کرو بازیگر آن بود و "ذهن زیبا" نام داشت را دیده ای؟ این فیلم را من تماشاکرده ام و موضوع کار برخی از دانشجویان ارشد و دکتری خودم قرار دادم.

من به خاطر آوردم که این فیلم را دیدم ولی هرگز کنجکاوی نکردم که "جان نش" که نقش ان را راسل کرو بازی می کرد و داستان زندگی واقعی این ریاضیدان بود که توانست جایزه ی نوبل ریاضی را از ان خود کند در حقیقت روی چه موضوعی از ریاضی کار می کرد؟

چرا تا به آن روز کنجکاوی نکرده بودم اصلا مهم نبود. مهم این بود که استاد خیلی خیلی کنجکاو و جسور بود و من بسیار بسیار تشنه بودم.

رفتم و تحقیقم را از کتاب های اقتصاد آغاز کردم. کتاب "اقتصاد ریاضی، روشها و کاربردها" نوشته ی "علی سوری" فصل های اخر را مطالعه کردم و فهمیدم دقیقا درست آمده ام.

در پست بعدی مقدمه ی کوتاهی از آنچه خوانده ام را بیان می کنم که می تواند "گامی کوچک اما شیرین در نظریه بازیها" باشد